ریاضیدان
-
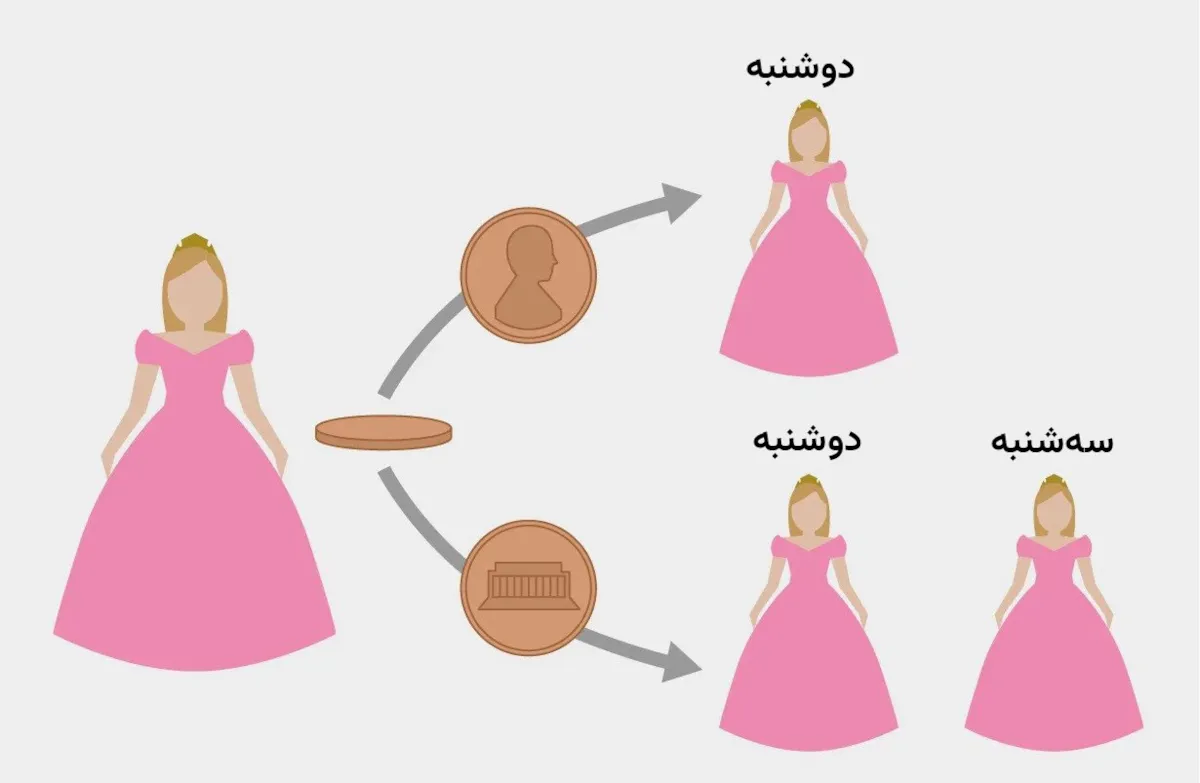
معمولا پاسخها در ریاضیات واضح هستند بهویژه اگر عملیات چندان پیچیده نباشد؛ اما دربارهی مسئلهی «زیبای خفته» که در سال ۲۰۰۰ به شهرت رسید، هیچ توافق جهانی وجود ندارد. کارشناسان فلسفه و ریاضیات به دو گروه تقسیم شدهاند و هر کدام با آوردن دلایل قانعکننده سعی میکنند نظریهی خود را ثابت کنند. بیش از ۱۰۰ مقالهی تخصصی دربارهی این معما وجود دارند و تقریبا هر شخصی که دربارهی آزمایش فکری زیبای خفته میشنود، نظریهی قوی خود را ارائه میکند. به نوشته وبسایت ساینتیفیک امریکن، مسئلهی زیبای خفته به این شرح است: زیبای خفته موافقت میکند در آزمایشی شرکت کند. او روز یکشنبه، یک قرص خواب میخورد و به خواب میرود. یکی از آزمایشگرها سکهای میاندازد اگر شیر بیاید، دانشمندان روز دوشنبه زیبای خفته را بیدار میکنند. سپس قرص خواب دیگری به او میدهند؛ اما اگر خط بیاید، زیبای خفته را روز دوشنبه بیدار میکنند، دوباره او را به خواب میبرند و سپس روز سهشنبه بیدارش میکنند. سپس قرص خواب دیگری به او میدهند. در هر دو سناریو، زیبای خفته روز چهارشنبه از خواب بیدار میشود و آزمایش به پایان میرسد. نکتهی مهم این است که زیبای خفته به دلیل مصرف داروی خواب، به یاد نمیآورد که قبلا از خواب بیدار …
-
غزال زیاری– قضیه فیثاغورث که در قرن ششم قبل از میلاد مسیح توسط فیثاغورث، ریاضیدان یونانی کشف شده بود، سنگ بنای ریاضیات است. فرمول این قضیه a۲ + b۲ = c۲ است و بر این فرض است که مجموع a۲ و b۲ که دو ضلع کوتاهتر یک مثلث قائمالزاویه هستند، برابر با c۲ که وتر مثلث است خواهد بود. در طول قرنها، این ایده توسط برترین نخبههای تاریخ، مانند آلبرت اینشتین، جیمز گارفیلد (رئیس جمهور اسبق آمریکا) و حتی خود فیثاغورث اثبات شده است. در حقیقت صدها اثبات برای قضیه فیثاغورث وجود دارد که اگر نه همه آنها، بله اکثرشان به طور مستقل نتوانستهاند تا با استفاده از مثلثات آن را اثبات کنند. دلیل این موضوع این است که مبانی این قضیه، چیزی است که کل حوزه مثلثات برپایه آن بنا شده است. از همین رو، استفاده از مثلثات برای اثبات این قضیه، به کارگیری چیزی است که “استدلال دایرهای” نامیده میشود. برخی ریاضیدانان بر این باور بودند که اثبات مستقل قضیه فیثاغورث از طریق مثلثات تقریبا غیرممکن است؛ یکی از آنها الیشا لومیس است که در کتابش در این زمینه (که یک قرن پیش منتشر شد) به این نکته اشاره کرده که هیچ برهان مثلثاتی وجود ندارد؛ چرا که …