چرا مسئله «زیبای خفته» ریاضیدانها را بیدار نگهداشته است؟
معمولا پاسخها در ریاضیات واضح هستند بهویژه اگر عملیات چندان پیچیده نباشد؛ اما دربارهی مسئلهی «زیبای خفته» که در سال ۲۰۰۰ به شهرت رسید، هیچ توافق جهانی وجود ندارد. کارشناسان فلسفه و ریاضیات به دو گروه تقسیم شدهاند و هر کدام با آوردن دلایل قانعکننده سعی میکنند نظریهی خود را ثابت کنند. بیش از ۱۰۰ مقالهی تخصصی دربارهی این معما وجود دارند و تقریبا هر شخصی که دربارهی آزمایش فکری زیبای خفته میشنود، نظریهی قوی خود را ارائه میکند.
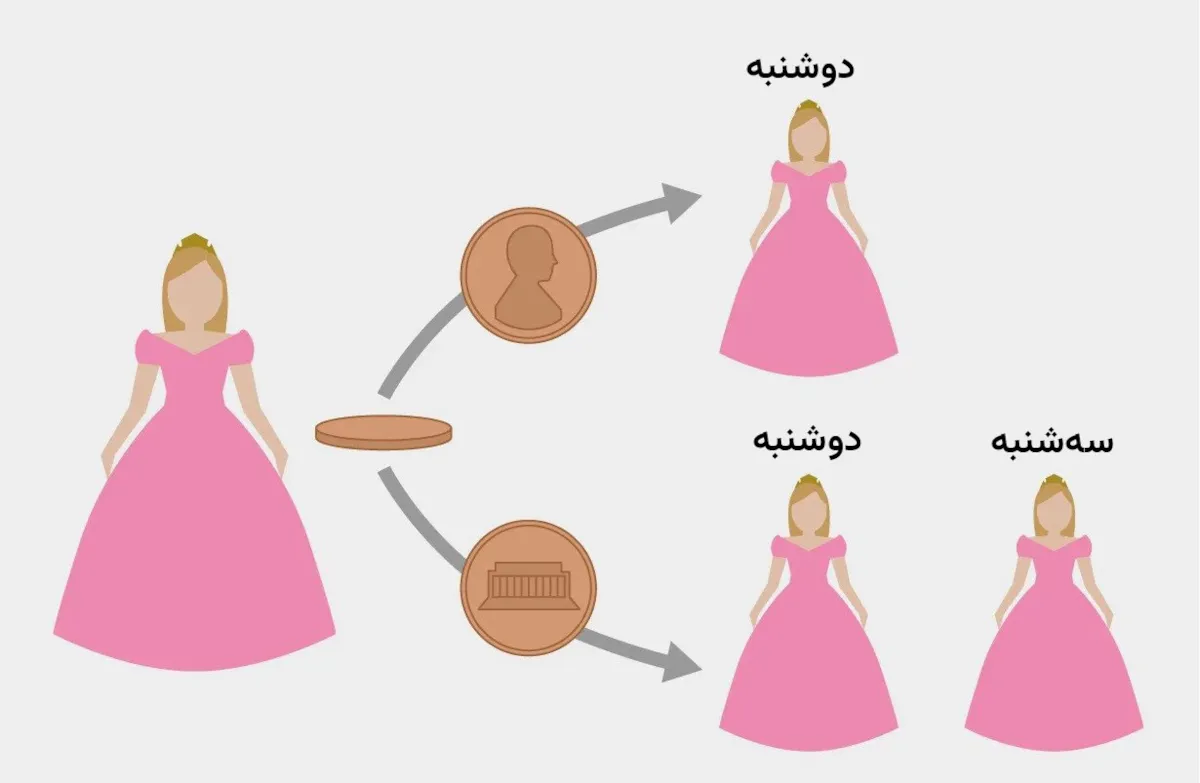
به نوشته وبسایت ساینتیفیک امریکن، مسئلهی زیبای خفته به این شرح است: زیبای خفته موافقت میکند در آزمایشی شرکت کند. او روز یکشنبه، یک قرص خواب میخورد و به خواب میرود. یکی از آزمایشگرها سکهای میاندازد اگر شیر بیاید، دانشمندان روز دوشنبه زیبای خفته را بیدار میکنند. سپس قرص خواب دیگری به او میدهند؛ اما اگر خط بیاید، زیبای خفته را روز دوشنبه بیدار میکنند، دوباره او را به خواب میبرند و سپس روز سهشنبه بیدارش میکنند. سپس قرص خواب دیگری به او میدهند. در هر دو سناریو، زیبای خفته روز چهارشنبه از خواب بیدار میشود و آزمایش به پایان میرسد.
نکتهی مهم این است که زیبای خفته به دلیل مصرف داروی خواب، به یاد نمیآورد که قبلا از خواب بیدار شده است؛ بنابراین وقتی بیدار میشود نمیتواند دوشنبه و سهشنبه را تفکیک کند. آزمایشگرها به زیبای خفته دربارهی نتیجهی سکه انداختن یا روز هفته، چیزی نمیگویند و فقط هر بار که از خواب بیدار میشود از او یک سؤال میپرسند: چقدر احتمال دارد که سکه به حالت «شیر» بیاید؟
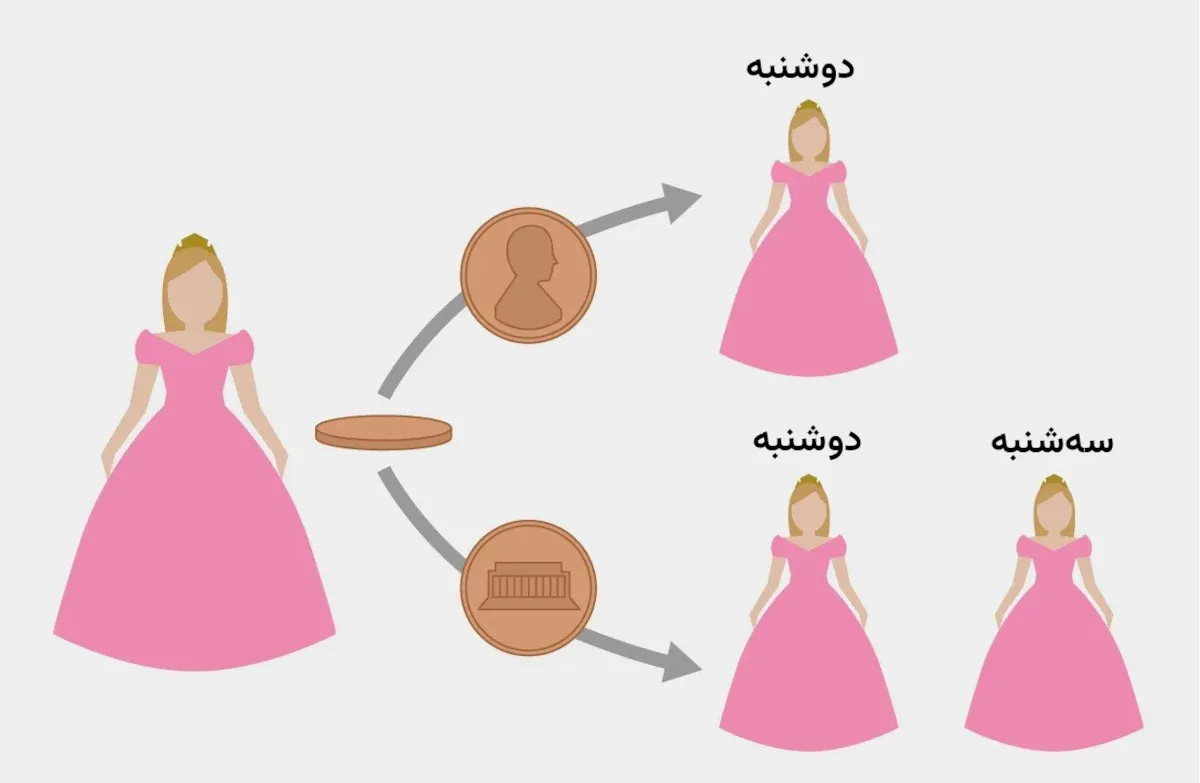
حالا خود را به جای زیبای خفته بگذارید. بیدار میشوید. نمیدانید چه روزی است و حتی نمیدانید قبلا بیدار شدهاید. تنها دربارهی مسیر تئوری آزمایش میدانید. در اولین سناریو، حدس زیبای خفته باید دارای احتمال ۱٫۲ باشد. احتمال سقوط سکه روی شیر یا خط صرفنظر از ادامهی آزمایش همیشه پنجاه درصد است. دیوید لوییس، فیلسوف آمریکایی هم همین عقیده را دارد. از طرفی میتوان سکه را پیش از به خواب بردن زیبای خفته انداخت. بر اساس طراحی آزمایش، زیبای خفته هیچ سرنخ اضافهای دربارهی موقعیت ندارد بنابراین از دیدگاه منطقی باید با احتمال ۱٫۲ حدس بزند.
اما فرضیههایی دربارهی احتمال ۱٫۳ هم وجود دارند. اگر با دقت به آزمایش زیبای خفته فکر کنید، سه سناریو رخ میدهند:
او روز دوشنبه بیدار میشود، سکه روی شیر ظاهر میشود.
او روز دوشنبه بیدار میشود، سکه روی خط ظاهر میشود.
او روز سهشنبه بیدار میشود، سکه روی خط ظاهر میشود.
احتمال هر رویداد چقدر است؟ میتوانید این احتمالها را بهصورت تجربی یا بر اساس ریاضیات بررسی کنید. فرض کنید سکهای را صد بار به هوا پرت میکنید و ۲۵ بار خط و ۴۸ بار شیر میآورید. به بیان دیگر، سناریوی دوشنبه/شیر ۴۸ مرتبه، دوشنبه/خط و سهشنبه/خط هم هر کدام ۵۲ مرتبه رخ میدهند.
از آنجا که سهشنبه خط تابع دوشنبه/خط است، احتمالها برای هر سه رویداد برابر هستند و بنابراین باید ۱٫۳ باشند. وقتی زیبای خفته بیدار میشود و از او خواسته میشود احتمال پرتاب سکه را حدس بزند، او با احتمال ۱٫۳ پاسخ میدهد.

آدام الگا، فیلسوف علم از دانشگاه پرینستون که مسئلهی زیبای خفته را در سال ۲۰۰۰ به شهرت رساند، به نتیجهی فوق رسید. او فرضیهی خود را بر اساس ریاضیات هم تعریف کرد اگر هنگام بیدار شدن به زیبای خفته بگوییم که امروز دوشنبه است (M) احتمال دوشنبه/شیر (M,H) با احتمال دوشنبه/خط (M,Z) برابر است: P(M,H)=P(M,Z)=۱/۲، در این معادله P مخفف احتمال است. از سوی دیگر اگر زیبای خفته پس از بیدار شدن متوجه شود سکه روی خط افتاده است، آن روز برابر است با دوشنبه یا سهشنبه (T) یا به عبارت دیگر P(M,Z)=P(T,Z)=۱/۲.
بر اساس محاسبهی احتمالهای شرطی، بهطورکلی (بدون اینکه زیبای خفته اطلاعات اضافهای دریافت نکند)، سه احتمال با یکدیگر برابر هستند: P(M,Z)=P(M,H)=P(T,Z). ازآنجاکه جمع سه احتمال باید برابر با عدد ۱ شود، بنابراین مقدار هر کدام ۱٫۳ است. از دید الگا، زیبای خفته در صورت قرار گرفتن سکه روی خط بیدار میشود و باید پاسخی با احتمال ۱٫۳ را ارائه کند.
اما چگونه میتوان پرسش را با توجه به دو فرضیهی فوق پاسخ داد؟ برای رسیدن به درک بهتری از مسئلهی زیبای خفته، میتوان به نسخهی کرانیتری از آن فکر کرد. فرض کنید در نمونهی احتمال خطها، زیبای خفته بیدار میشود و نهتنها یک بار بلکه یک میلیون بار از او سوال میپرسند (با این فرض که این پرسش در بازههای زمانی کوچکتری رخ میدهد). اگر او را بیدار کنید و از او احتمال فرود آمدن سکه روی شیر را بپرسید، در این سناریو پاسخ ۱٫۲ به نظر منطقی نمیرسد. اگر نتیجهی پرتاب سکه خط باشد، از زیبای خفته یک میلیون بار به صورت متوالی سوال میپرسند و اگر شیر باشد، تنها یک بار از او پرسیده میشود.
اما نمونههای کرانی میتوانند جایگاه نظریهی ۱٫۲ را تقویت کنند. برای مثال، بهجای پرتاب سکه میتوان از مسابقهی ورزشی دوی یوسین بولت، دوندهی حرفهای در برابر تیلور سوییفت، خوانندهی پاپ، کمک گرفت. در این سناریو اگر بولت که رکورددار بسیاری از دستههای دو و میدانی است، تیلور سوییفت ستارهی پاپ را شکست دهد، زیبای خفته تنها یک بار روز دوشنبه بیدار میشود اما اگر برخلاف تمام انتظارات، سوییفت برنده شود، زیبای خفته هر روز به مدت یک ماه و سی مرتبهی متوالی بیدار میشود. احتمال باخت بولت به سوییفت بسیار پایین است؛ اما اگر همان منطق پاسخ ۱٫۳ را به کار ببریم، باید با تمام سناریوها به شکلی یکسان برخورد کنیم. زیبای خفته باید پس از بیدار شدن روی پیروزی سوییفت شرط ببندد زیرا در این موقعیت بسیار بعید، ممکن است سی مرتبه بیدار شود. البته لویس این سناریو را مهمل میداند.
تا اینجای کار حتما خیلی گیج شدهاید؟ باید بگوییم تنها نیستید. آیا نظرتان تغییر کرد؟ با توجه به استدلالهای فوق شاید نتوان کاملا با پاسخ گروه ۲/۱ قانع شد از طرفی میتوان دیدگاههایی را از موقعیت ۳/۱ به دست آورد. این معما کاربردهای جالبی دارد. فیلسوفها و ریاضیدانها میتوانند از آن برای تصمیمگیری و احتمال به شکلی گسترده استفاده کنند. برای مثال، این آزمایش ذهنی نشان میدهد باورهای اشخاص (در این نمونه، زیبای خفته) میتواند به بیش از یک نتیجهگیری منطقی بینجامد. همچنین بر تفاوت بین تعداد احتمالهای آزمایشی (مثل به دست آمدن شیر در مقابل خط) و تجربههای محتمل شخص داخل آزمایش تأکید میکند.
۲۲۷۲۲۷